Abb.1: Zwei Möglichkeiten, einen Berg zu überwinden.

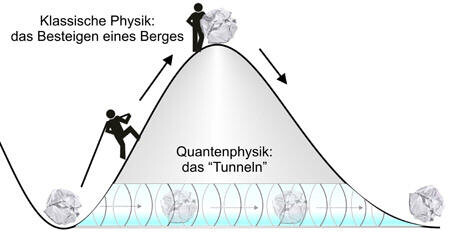
In der klassischen Physik muss man den Berg besteigen, um auf die andere Seite zu gelangen. In der Quantenphysik geht das jedoch auch anders: Objekte können den Berg einfach waagerecht durchqueren - sie tunneln. (Quelle: Max-Planck-Institut für Quantenoptik; zur externen Webseite der Quelleninformation).

Skalierung im Alltag - More is different

Skalierungs-Probleme nennt man Probleme, die sich durch die reine Vergrößerung oder Verkleinerung eines Systems ergeben können, und die sich nicht durch reine Vergrößerung bzw. Verkleinerung aller beteiligten Parameter lösen lassen. Dazu einige einfache Beispiele aus unserem normalen (beobachtbaren) Umfeld, z.B. aus dem sozialen Bereich:

• 3 Menschen verhalten sich ganz anders als 100 Menschen
• Einzelne Fische verhalten sich vollkommen anders als ein Schwarm Fische

z.B. aus dem technischen Bereich:

• Die Mischung von Substanzen ändert sich, ob sie nun im Mikromaßstab (Tropfen), Labormaßstab (Liter), Pilotmaßstab (Kubikmeter) oder im industriellen Maßstab (Tankfüllungen) durchgeführt werden
• Die elektrischen Eigenschaften von Strukturen auf einem Halbleiter ändern sich, wenn die Leiterbahnen einen immer geringeren Querschnitt bekommen

Skalierungsprobleme im Elektronikbereich

Während meiner seit mehr als 5 Jahren sehr intensiven Tätigkeit im Bereich der Entwicklung von Leistungselektronik für Hybrid- und Elektrofahrzeuge, bereitet mir die Skalierung dabei immer mehr Sorge. Um den Anforderungen an die Leistungselektronik gerecht zu werden, werden Schaltungen / Boards entwickelt, auf denen sich mehr als 1.000 Einzel-Komponenten die Arbeit teilen. Aktuell kommt es dabei häufiger vor, dass eine solche hochkomplexe Schaltung / Konfiguration / Architektur mit den bisher üblichen Methoden ausgelegt und getestet wird. Vollkommen unberücksichtigt ist dabei allerdings noch die Tatsache, dass sich solche komplexen Gesamt-Lösungen nicht einfach aus der Addition der Lösungen der Teilprobleme ergeben.

In der derzeitigen Vorgehensweise werden beispielsweise keine Wechselwirkungen zwischen den einzelnen (bekannten) Teilsystemen berücksichtigt. Durch labile Gleichgewichte in einzelnen Bereichen können sich daher schon durch geringste Ursachen vollkommen andere Effekte ergeben, an die keiner der Beteiligten auch nur im schlimmsten Alptraum gedacht hat.

Zur Verdeutlichung kann der Hinweis auf den so genannten "Schmetterlings-Effekt" bzw. der Gedanke an die Chaos-Theorie dienen. Gemeint ist damit, dass bei geringfügigsten geänderten Anfangsbedingungen eines Systems das Endergebnis vollkommen anderes aussehen kann bzw. wird. Im Falle des Schmetterlingseffekts sagt man, dass sich der Flug eines Schmetterlings auf der anderen Erdhalbkugel darauf auswirken könnte, ob ein Hoch- oder Tiefdruckgebiet entsteht.

Eine andere praktische Anschauung ist ein 2-Massen-Pendel. Wenn dieses aus (ersichtlich) gleicher Startposition losgelassen wird, wird es sich schon nach kurzer Zeit immer wieder vollkommen anders verhalten.

Abb. 2: Zweimasspendel, (Quelle: http://de.wikipedia.org/wiki/Datei:Zweimasspendel.png).

Mögliche Auswirkungen

Was können die möglichen Auswirkungen der immer komplexer werdenden Schaltungen sein?

1. Wir dürfen nicht davon ausgehen, dass sich zehn einzelne Schaltungsteile, die im Stand-Alone-Betrieb reibungslos funktionieren, auch im Zusammenhang problemlos arbeiten.
2. Auch kleine Abweichungen in den Bauteilen können für die Gesamtschaltung Fehler erzeugen, die in dem einzelnen Modul nicht auffällig geworden sind.
3. Um solche komplexen Schaltungen entsprechend testen zu können, muss in Zukunft immer mehr in die Betrachtung von Grenzmustern eingestiegen werden: hier müssen einzelne Parameter in möglichst vielen Kombinationen bis an die Grenzen der Toleranzen (und vielleicht auch noch darüber hinaus) simuliert werden.

Eine mögliche Lösung?

Eine Lösung für diese Probleme könnte die Definition von einheitlichen Schnittstellen / Interfaces zwischen den einzelnen Modulen / Schaltungsteilen sein. Dadurch könnten die Ausgangsgrößen der einzelnen Schaltungen so definiert werden, dass sie problemlos als Eingangsgrößen für andere Module verwendet werden können. Diese Vorgehensweise ist nun sicherlich nicht vollkommen neu, denn sie wird im Bereich der Mechanik schon seit vielen Jahren als Baukastenprinzip zur Anwendung gebracht. Aber im Bereich der Hardware (und teilweise auch Software) gibt es in diesem Bereich sicherlich noch einen ganz erheblichen Verbesserungsbedarf."